[adsense:responsibe:9545213979]
Mensaje de error
- Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en menu_set_active_trail() (línea 2394 de /home1/montes/public_html/drupal/includes/menu.inc).
- Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).
Se encuentra usted aquí
Apartada b) de la cuestion 2 EDiferenciales 1106S2 (Sistema Fundamental): Page 2 of 2
Solapas principales
Enviado por Anónimo (no verificado) en Mar, 05/20/2014 - 19:20
[adsense:336x280:9156825571]
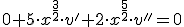
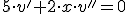
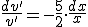
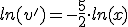
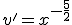
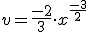
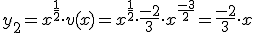
Programa en Sagemath para comprobar la resolucion de la funcion en la ecuacion diferencial
sage:var('x')
sage:v=-(2/3)*x^(-3/2)
sage:y=x^(1/2)*v
sage:f5=2*x^2*diff(y,x,x)+3*x*diff(y,x)-y
sage:f5.full_simplify()
Resultado de la funcion con Sage
0
Las dos soluciones son linealmente independientes y como el sistema es de orden 2 es el sistema fundamental.
Tags:
Español
google+:
Páginas

Búsqueda personalizada
Idiomas
 English
English Español
Español
Comentarios recientes
- Muy bueno hace 10 años 1 mes
- good hace 10 años 2 meses
- Engranajes hace 10 años 2 meses
- REVISAR hace 10 años 3 meses
- UTIL hace 10 años 3 meses
- Realimentación hace 10 años 5 meses
- Hello There. I found your hace 10 años 6 meses
- Good web site! I really love hace 10 años 6 meses
- Well I really enjoyed reading hace 10 años 6 meses
- Thanks again for the blog hace 10 años 6 meses
Seguidores en Google
Busquedas populares
Inicio de sesión
Contenido popular
- Tema 5: Cinematica del solido rigido
- AYUDA SOLIDWORKS MOTION
- TALLER 3 DE GEOGEBRA 4
- Ejercicio Resuelto
- Leccion 8 Tablas en Latex
- Sensores inteligentes
- RELACIÓN DE PROBLEMAS DE CINEMÁTICA DE MECANISMOS
- Apuntes de GeoGebra con unos puntos de Mates
- Mecanica II
- Working Model Tutorial
- Mecanismos de Movilidad
- Examen 2011 Septiembre 2 semana
- 1 Cuestion 1 (Diodos, portadores)
- Capitulo2 diagrama de bloques
- Parte practica S.POTENCIA 2013 09 S2 (Tiempo medio entre fallos)
- TUTORIAL 2 – WORKING MODEL 2D
- Dibujando en SolidWorks (Ingles)
- Contaminacion en la forja y fundicion
- Tema 4: Vectores deslizantes
- 2.- Vectores deslizantes.
- TUTORIAL 3 – WORKING MODEL 2D
- Balanceo de maquinaria oscilante (Ingles)
- Mecanismos. Engranajes
- Modelado matemático de los sistemas dinámicos
- FINAL DE SEPTIEMBRE SERVOSISTEMAS
Páginas
Today's popular content
- Apartada c) de la cuestion 2 EDiferenciales 1106S2 (Wronskiano)
- Cuestion 2 EDiferenciales 1109S1 (Ecuacion diferencial de Euler)
- EDiferenciales 1206S2
- Cuestion 1 EDiferenciales 1206S2 (Ecuacion diferencial exacta; Factor integrante)
- Apartada a) de la cuestion 1 EDiferenciales 1206S2 (Ecuacion diferencial exacta)
- Apartada b) de la cuestion 1 EDiferenciales 1206S2 (Factor integrante, Ecuacion diferencial exacta)
- Cuestion 2 EDiferenciales 1206S2 (Ecuacion diferencial lineal; Punto ordinario)
- Apartada a) de la cuestion 2 EDiferenciales 1206S2 (Ecuacion diferencial lineal; Punto ordinario)
- Apartada b) de la cuestion 2 EDiferenciales 1206S2 (Ecuacion diferencial lineal; Desarrollo en serie)
- EDiferenciales 1209S1
- Cuestion 1 EDiferenciales 1209S1 (Ecuacion diferencial de Clairaut)
- Apartada a) de la cuestion 1 EDiferenciales 1209S1 (Ecuacion diferencial de Clairaut)
- Apartada b) de la cuestion 1 EDiferenciales 1209S1 (Ecuacion diferencial de Clairaut, solucion singular, envolvente)
- Cuestion 2 EDiferenciales 1209S1 (Ecuacion diferencial lineal homogenea de coeficientes constantes, Wronskiano)
- Apartada a) de la cuestion 2 EDiferenciales 1209S1 (Wronskiano)
- Apartada b) de la cuestion 2 EDiferenciales 1209S1 (Ecuacion diferencial lineal homogenea)
- Apartada c) de la cuestion 2 EDiferenciales 1209S1 (Ecuacion diferencial lineal de coeficientes constantes)
- Cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes)
- Apartada a) de la cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes, solucion general)
- Apartada b) de la cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes, solucion particular)
- Apartada c) de la cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes, estabilidad)
- EDiferenciales 1406S2
- Cuestion 1 EDiferenciales 1406S2 (Ecuacion diferencial exacta; Factor integrante)
- Apartada a) de la cuestion 1 EDiferenciales 1406S2 (Ecuacion diferencial exacta)
- Apartada b) de la cuestion 1 EDiferenciales 1406S2 (Ecuacion diferencial exacta, Factor integrante)
Páginas
Matematicas
- Derivadas
- Ecuaciones Diferenciales
- Aclaraciones en libro de Ecuaciones Diferenciales
- Apuntes y enlaces de Ecuaciones Diferenciales
- Examenes de Ecuaciones Diferenciales
- Resumen de tipos de Ecuaciones Diferenciales
- Estadistica
- INTEGRALES
- Operaciones con logaritmos
- Operaciones con nabla, productos vectoriales y escalares
- Operaciones con complejos


Añadir nuevo comentario